در ادامه مبحث استخراج معادلات المان ها در روش اجزاء محدود، در این بخش ما قصد داریم درباره رویکرد عددی صحبت کنیم. همانگونه که در مقاله قبل ذکر شد این رویکرد در حل مسائل بسیار پیچیده تر به ما کمک می کند. در این رویکرد لازم است ابتدا معادلات حاکم بر سیستم را بشناسیم. به استثناء مسائل ساده، معمولا حل این معادلات به سادگی امکان پذیر نیست از این رو به این حالت از معادلات Strong Form گفته می شود. با توجه به این موضوع، با استفاده از یک سری اصول ریاضی این معادلات را به شکل انتگرالی در می آوریم تا به Weak Form معادلات دست پیدا کنیم که کار با آنها راحت تر است. این نگرش کلی استخراج معادلات اجزاء محدود است که در این مقاله به توضیح آن پرداخته می شود.

یافتن معادله حاکم بر سیستم (معادله دیفرانسیل سیستم)

برای درک بهتر از رویکرد عددی در استخراج معادلات اجزاء محدود روی مثالی که در شکل 1 نشان داده شده است کار می کنیم. مانند قبل با میله ای که از سه بخش با سطح مقطع متغیر تشکیل شده مواجه ایم. در این مثال نیروی گسترده b(x) در طول میله اعمال شده که واحد آن، نیرو بر طول است. همچنین یک نیروی متمرکز F نیز به سر تیر اعمال شده و در حال کشش کل تیر است.

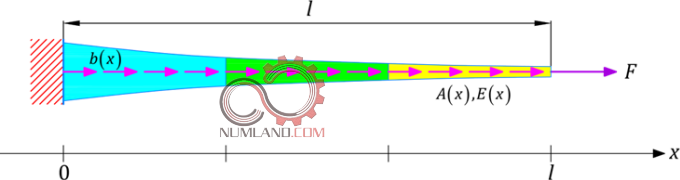
همان طور که در شکل 2 نشان داده شده است همیشه برای استخراج معادلات دیفرانسیل یک سیستم نیاز به بررسی یک برش از آن به طول dx می باشد. همانگونه که در شکل 3 مشخص است، این برش از نقطه x شروع شده و در نقطه x+dx پایان می پذیرد.

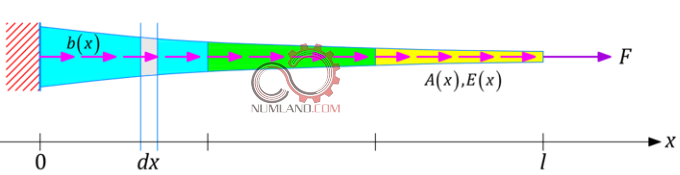
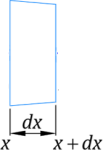
به عنوان اولین قدم نیروهای حاکم بر این برش را بررسی کرده و معادلات تعادل را برای آن می نویسیم. همانطور که در شکل 4 نشان داده شده است نیروی گسترده اعمال شده روی این بخش از میله را میانگین نیروی گسترده و برابر 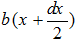در نظر می گیریم. از طرفی هم نیروهای متمرکز p(x) و p(x+dx) به دو طرف المان وارد می شود.