در مقاله های قبل به این بحث پرداختیم که برای حل مسائل پیچیده ابتدا هندسه مسئله را گسسته می کنیم تا با تقسیم مسئله به قطعات کوچکتر بتوانیم پاسخ مسئله را تخمین بزنیم. در این راستا دو رویکرد مستقیم و عددی را معرفی کردیم. دیدیم که برای حل یک مسئله در رویکرد دوم نیازمند بدست آوردن معادله حاکم بر سیستم با در نظر داشتن شرایط مرزی هستیم. در مسائل ساده این معادله می تواند به راحتی حل شود، اما در مسائل پیچیده ناگزیر به حل معادلات به روش های عددی هستیم. به همین دلیل هم این رویکرد را عددی نام گذاری کرده اند.
از آنجا که حل دقیق معادله دیفرانسیل حاکم بر سیستم سخت است، آن را با نام Strong Form شناختیم. توضیح دادیم به منظور حل عددی این حالت از معادله، آن را تبدیل به Weak Form می کنیم. بدین منظور معادله دیفرانسل را به جای مساوی قرار دادن با 0، برابر مقداری که به آن Residual گفتیم در نظر می گیریم و با استفاده از روش های عددی سعی بر کمینه کردن آن می کنیم.
روش های عددی مختلفی که به Weighted Residual Methods نام گذاری شده اند بدین منظور می توانند استفاده گردند. همانگونه که عنوان شد در این میان Galerkin’s Method در روش اجزاء محدود استفاده می شود. در نهایت نیز گفتیم بسط معادلات Galerkin که بصورت انتگرالی از ضرب Residual در Weight بود، مارا به طور خاص در مسائل الاستیک خطی به معادلات انرژی پتانسیل کمینه می رساند. به عبارت دیگر حالت Weak Form در مسائل الاستیک خطی با معادلات انرژی پتانسیل کمینه معادل است. به زبان ساده این بدان معنی است که اگر ما به جای طی کردن تمام این فرآیند، معادله انرژی پتانسیل جسم را بدست آورده و آن را کمینه کنیم عملا به معادله Weak Form که در واقع تخمینی از Strong Form است خواهیم رسید.
توضیح اینکه تابع تخمین u(x) می تواند یک تابع کلی در بازه 0 تا L باشد که ضرایب ci در آن مجهول است. با محاسبه انرژی پتانسیل بر اساس این تابع و کمینه کردن آن می توانیم این ضرایب را بیابیم. اما در روش اجزاء محدود یاد گرفتیم برای تحلیل مسائل پیچیده می توانیم آن ها را به قسمت های ریزتر تقسیم بندی، گسسته سازی و یا مش بندی کنیم. با توجه به رویکردی که از محاسبه تابع تخمین گفتیم می توانیم در هریک از این المان ها، یک تابع مجزا (و شاید مشابه) پیشنهاد دهیم. سپس با توجه به این توابع، انرژی پتانسیل را برای کل سیستم بدست آورده و در نهایت ان را کمینه کنیم.
به عبارت دیگر رویکرد المان محدود بدین گونه است که به جای آنکه کل مسئله را یک جا و با یک تابع (مثلا u(x)) بصورت تقریبی حل کنیم، مسئله را گسسته کرده و برای هرکدام از المان ها یک u(x) پیشنهاد داده و انرژی پتانسیل را برای آن پیدا کرده و کمینه می کنیم.
انرژی پتانسیل کمینه
اکنون می خواهیم با نحوه محاسبه انرژی پتانسیل آشنا شویم. همان طور که در رابطه پایین نشان داده شده است انرژی پتانسیل برابر با اختلاف انرژی کرنشی و کار خارجی است.
Π(G)=Λ(G)-W(G)
طبق تعریف، انرژی کرنشی در واحد حجم برابر است با سطح زیر نمودار تنش-کرنش. بدین معنی که اگر از رابطه تنش کرنش روی حجم انتگرال بگیریم به انرژی کرنشی کل خواهیم رسید. کار یک نیروی خارجی هم طبق تعریف برابر ضرب داخلی نیرو در جابجایی آن است. قاعدتا کار کل نیروهای خارجی مجموع کار تمام نیروهای خارجی می باشد.
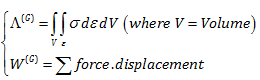
انرژی کرنشی سیستم
اکنون برای به دست آوردن انرژی کرنشی روابط زیر را دنبال کنید.
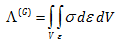
طبق تعریف در مسائل الاستیک خطی و در میله تحت کشش، قانون هوک رابطه بین تنش و کرنش را بصورت σ=Eε مشخص می کند. از طرفی برای یک میله با سطح مقطع A، رابطه dV=A.dX برقرار است. به این ترتیب رابطه انرژی کرنشی کل به شکل زیر می تواند نوشته شود:
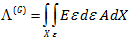
در این مرحله می توان از کرنش انتگرال گرفت و به رابطه زیر رسید:
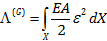
از قبل می دانیم که ε مشتق جابجایی هاست. به این ترتیب اگر معادله جابجایی u(x) میله را بیابیم، با یک بار مشتق گرفتن از آن به معادله کرنش می رسیم. با داشتن کرنش طبق رابطه بالا انرژی کرنشی کل را نیز می توانیم محاسبه نماییم. بنابراین با فرض داشتن میزان کار خارجی، انرژی پتانسیل کل به دست می آید. با توجه به این موضوع، کاری که ما در ادامه انجام می دهیم این است که u(x) را به صورت پارامتری در نظر بگیریم. سپس پارامترهای گفته شده در بالا را بر این اساس محاسبه کرده و در نهایت پارامترهای موجود در u(x) را طوری بدست آوریم که انرژی پتانسیل کل سیستم، کمینه شود. پس در مرحله اول و با توجه به رویکرد عددی که در مقاله قبل توضیح دادیم، بایستی معادلاتی برای u(x) پیشنهاد دهیم.
یافتن رابطه جابجایی روی المان ها به عنوان پیشنهادی برای تابع u(x)
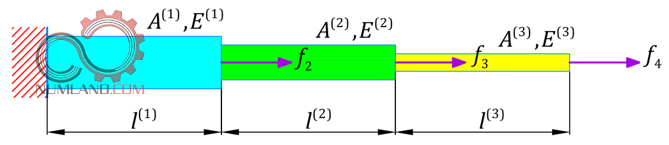
برای درک بهتر، مراحل گفته شده را برای مثال زیر دنبال می کنیم. همانطور که در شکل 1 می بینید یک میله در حال کشش داریم که از سه بخش تشکیل شده و هر بخش سطح مقطع، مدول الاستیسیته و طول مخصوص به خود را دارد. همچنین سر هر بخش یک نیروی متمرکز کششی اعمال شده است.
مطابق شکل 2 می بینید مسئله را گسسته کرده و روی هر گره یک جابجایی در نظر می گیریم. همانگونه که مشاهده می شود، میله از 4 گره تشکیل شده است که 3 المان بین آن ها قرار گرفته اند. گره ها را با n و المان ها را e نشان داده ایم. همچنین u نمایانگر جابجایی مربوط به هر گره است.
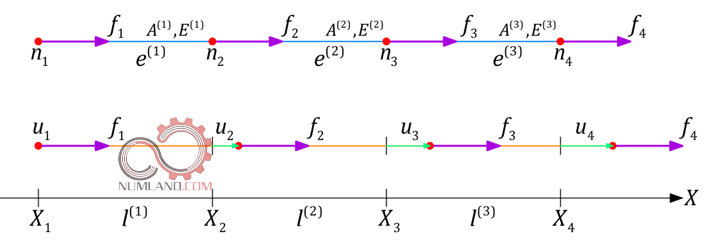
از بحث گسسته سازی در شکل 3 از مقاله اول داشتیم که اگر ما هر یک ازین جابجایی ها را محاسبه کرده و فرض کنیم بین آنها یک رابطه خطی وجود دارد، با رسم خطوط بین گره ها نمودار یا پروفیل u(X) بدست می آید.
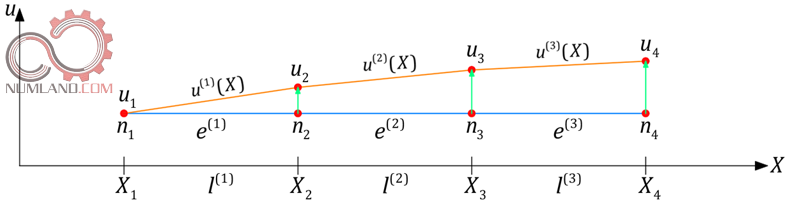
همانطور که در شکل 3 می بینید برای هر المان یک رابطه جابجایی داریم که در شکل با u(1)(X)، u(2)(X) و u(3)(X) نشان داده شده است. در واقع این توابع همان توابعی هستند که گفتیم در قدم اول رویکرد عددی پیشنهاد می دهیم.
دقت کنید در تمامی نامگذاری ها در این مقاله، شماره المان همواره به صورت توان و شماره گره ها به صورت اندیس نمایش داده می شود. به عنوان مثال u(e)(X) بیانگر معادله جابجایی در المان e و ui به معنی جابجایی گره i ام است. در روش اجزاء محدود، اکثر اوقات، معادله پیشنهادی جابجایی برای تمام المان های مشابه یکسان در نظر گرفته می شود. بنابراین برای استخراج این معادله، یک المان را مانند شکل 4 در نظر می گیریم.
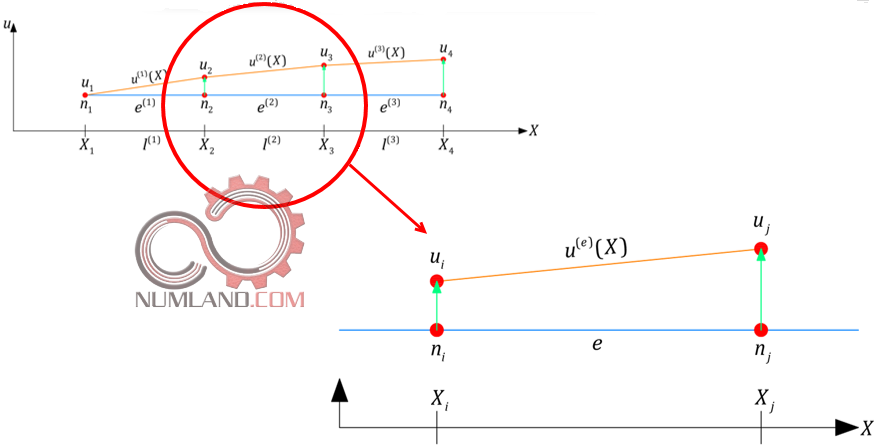
اگر المان e با گره های ni و nj به ترتیب در سمت چپ و راست المان را در نظر بگیرید که هریک ازین گره ها قرار است جابجایی ui و uj را داشته باشند در نهایت به معادله u(x) می رسیم که مربوط به المان e است. از آنجا که قصد داریم معادله ای که بدست می آوریم را روی تمام المان ها اعمال کنیم، بنابراین بجای استفاده از مختصات کلی (Global) یک مختصات محلی (Local) روی المان تعریف می نماییم:

در این مختصات نقطه صفر را روی گره سمت چپ لحاظ می کنیم. l(e) طول المان بوده که برابر با تفاضل Xj و Xi می باشد. دقت کنید X (ایکس بزرگ) برای مختصات کلی و x (ایکس کوچک) برای مختصات محلی در نظر گرفته شده است. به این ترتیب المان e در بازه زیر تعریف می شود:
Xi≤X≤Xj or 0≤x≤l(e)
با توجه به خطی بودن رابطه بین دو گره i و j که در شکل ها مشهود است می توانیم معادله خط زیر را برای آن پیشنهاد دهیم.
u(e)(X) =c1+c2X
از طرفی شرایط مرزی زیر را برای این معادله داریم:
u(e)(Xi) =ui, u(e)(Xj) =uj
دقت کنید در اینجا ما عملا ui و uj را معلوم فرض کرده ایم گرچه مقدار آن را نمی دانیم و بعدا در روند حل مسئله به روش اجزاء محدود مقادیر آنها را خواهیم یافت. با جایگذاری شرایط مرزی در معادله اصلی به یک دستگاه معادلات دو مجهولی می رسیم که با حل آن مقادیر ci و cj قابل استخراج هستند.
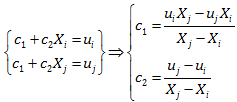
با جایگذاری این مقادیر، معادله اصلی به شکل استاندارد زیر در می آید:
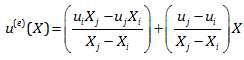
از آن جا که قصد داریم روی پارامتر های ui و uj کار کنیم، معادله بالا را بر حسب این پارامترها مرتب می کنیم:
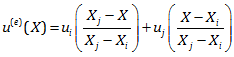
در این رابطه توابعی که به ui و uj ضرب شده اند را به ترتیب Si(e) و Sj(e) می نامیم. توجه داشته باشید تابع u(e)(X) از مجموع دو تابع چند جمله ای (Si(e), Sj(e)) ضرب در دو ضریب مجهول (ui و uj) ایجاد شده است. این همان رابطه u(x) است که در رویکرد عددی در مقاله قبل به عنوان روش عددی پیشنهاد شد. یعنی رابطه:
u(x) =Σ ciϕi(x)
اکنون معادلات Si(e) و Sj(e) را بر اساس مختصات محلی بازنویسی می نماییم.
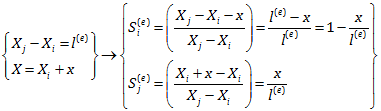
پس در نهایت داریم:
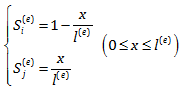
به نمودار زیر که رفتار توابع بدست آمده را نشان می دهد توجه کنید. همانگونه که مشاهده می کنید در گره i مقدار Si(e) برابر یک و مقدار Sj(e) برابر صفر است. اما، برعکس، مقادیر این توابع در گره j به ترتیب صفر و یک خواهند بود. همچنین بین این دو مقدار، هر دو تابع به صورت خطی تغییر می کنند. در روش اجزاء محدود به این توابع اصطلاحاً Shape Function گفته می شود. با استفاده از این توابع می توان بین ui و uj درون یابی مقدار جابجایی را درون یابی نمود.
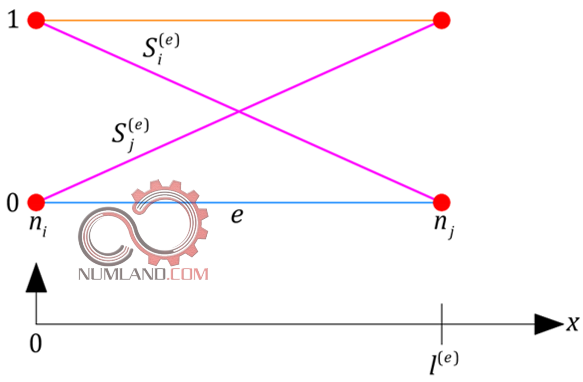
به هر حال از بالا داریم:
u(e)(x) = uiSi(e) + ujSj(e)
به این دلیل که در اینگونه مسائل، کار کردن با ماتریس ها نسبت به حالت اسکالر بسیار راحت تر خواهد بود، بنابراین معادله بالا را در فرم ماتریسی دنبال می کنیم. پس معادله بالا را به شکل زیر بازنویسی می کنیم:
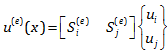
طبیعتا حاصل ضرب این دو ماتریس معادله u(e)(X) را به ما می دهد. با جایگذاری Si(e) و Sj(e) از مرحله قبل به شکل جدید این معادله می رسیم.
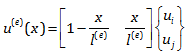
ارتباط انرژی کرنشی کل و انرژی کرنشی المان ها
اکنون رابطه ای که می خواستیم برای جابجایی ها در المان e پیشنهاد بدهیم را داریم. پس به سراغ کرنش می رویم و بعد از محاسبه کرنش با به دست آوردن انرژی کرنشی بخشی از معادله انرژی پتانسیل را محاسبه کنیم.
از قبل فهمیدیم انرژی کرنشی کل در یک میله از رابطه زیر به دست می آید:
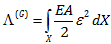
در اینجا ε کرنش، E مدول الاستیسیته و A سطح مقطع میله است.
همان طور که در شکل 7 هم می بینید حدود انتگرال از X1 تا X4 در مختصات کلی (گلوبال) تغییر خواهد کرد.

اما با توجه به اینکه رابطه u(e)(X) در مختصات محلی بدست آمده بود، مختصات را مطابق شکل 8 بصورت محلی در نظر می گیریم.
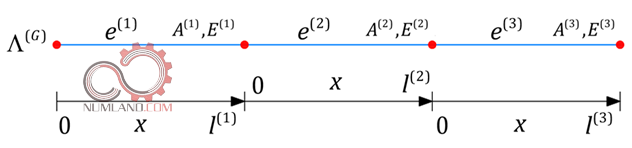
بنابراین با انتگرال گیری بر اساس این مختصات داریم:
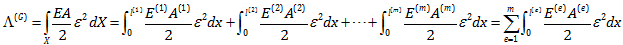
بدین ترتیب انتگرال انرژی کرنشی کل را به انتگرال روی المان ها خرد کرده ایم. به عبارت دیگر روی هر المان یک انتگرال داریم. اگر کرنش مربوط به هر المان را بدست آوریم، با توجه به اینکه E و A روی هر المان مشخص است، می توانیم انتگرال روی هر المان را محاسبه نماییم. از طرف دیگر می توان گفت حاصل این انتگرال انرژی کرنشی است که المان e در خود ذخیره کرده است. یعنی:
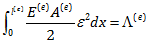
پس برای انرژی کرنشی کل داریم:
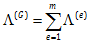
به عبارت دیگر می توان گفت انرژی کرنشی کل سیستم برابر با مجموع انرژی کرنشی های تمام المان ها می باشد.
کار نیروی خارجی
همانگونه که در بالا گفته شد، کار نیروی خارجی که بخش دوم معادله انرژی پتانسیل است برابر با مجموع ضرب داخلی نیروهای خارجی در جابجایی مربوطه در هر گره است. اگر این بحث را مانند شکل 9 روی یک گره بررسی کنیم که در آن نیروی خارجی fi روی گره ni با جابجایی ui اعمال شده است، کار نیروی خارجی روی این المان به شکل زیر خواهد بود:
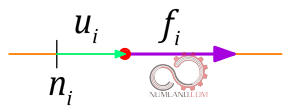
W(i)=fi ui
و اگر مطابق شکل 10 کل سیستم را در نظر بگیریم، کار کل نیروهای خارجی برابر خواهد بود با:

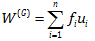
محاسبه انرژی پتانسیل و نحوه کمینه کردن آن
به منظور یادآوری آنچه تا کنون آموخته ایم روابط زیر را دنبال کنید.
Π(G)=Λ(G)-W(G)
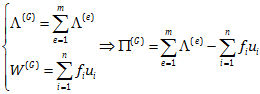
از طرفی می دانیم طبق تئوری انرژی پتانسیل کمینه، معادلات حاکم بر سیستم در حال بررسی وقتی ارضا می شود (سیستم وقتی به تعادل می رسد) که Π(G) در کمترین مقدار خود باشد. با توجه به این موضوع ضرایب مجهولی که در تابع پیشنهادی u(x) در نظر گرفته بودیم را طوری بدست می آوریم که انرژی پتانسیل سیستم کمینه شود. همچنین در این مقاله معادلات را طوری نوشتیم که ضرایب مجهول در u(x) همان جابجایی گره ها یعنی ui و uj هستند.
با توجه به صحبت بالا هدف ما پیدا کردن جابجایی های u به نحوی است که انرژی پتانسیل کل کمینه باشد. برای این کار لازم است از انرژی پتانسیل نسبت به جابجایی تمام گره ها مشتق گرفته و برابر صفر قرار دهیم. البته اثبات این موضوع در این بحث نمی گنجد اما بایستی اشاره کنیم که اکسترمم انرژی پتانسیل می نیمم است. بنابراین به تعداد جابجایی گره ها معادله خواهیم داشت. اگر فرض کنیم n گره داشته باشیم، با توجه به اینکه روی هر گره یک جابجایی درنظر گرفته ایم، بنابراین با مشتق انرژی پتانسیل کل نسبت به هر کدام از جابجایی ها n معادله به شکل زیر خواهیم داشت.

در نظر داشته باشید به دلیل خطی بودن روابط انرژی کرنشی و کار نیروی خارجی با انرژی پتانسیل به راحتی می توانیم مشتق انرژی پتانسیل را با تفاضل مشتق انرژی کرنشی و کار نیروی خارجی معادل قرار دهیم.
همچنین پارامتر uq نمادی از جابجایی گره ها است. در ادامه جابجایی ها را در معادلات با این نماد می نویسیم و در نهایت به q مقدارهای 1 تا n را می دهیم تا جابجایی کل گره ها را در نظر بگیریم.
بهترین کار برای اینکه این دستگاه معادلات را حل کنیم این است که آن را از حالت اسکالر به حالت ماتریسی بنویسیم.

از قبل داریم:
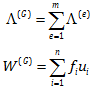
و از طرفی می دانیم در مورد عملگر Σ مشتق را می توانیم به داخل آن ببریم. این به این مفهوم است که مشتق انرژی کرنشی کل نسبت به uq برابر است با مجموع مشتق های انرژی کرنشی هر المان نسبت به uq به این ترتیب خواهیم داشت:
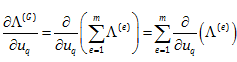
همچنین برای کارنیروی خارجی کل نیز داریم:
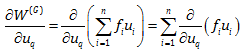
پس در مراحل بعد هدف محاسبه مشتق انرژی کرنشی در المان e و مشتق ضرب داخلی نیرو و جابجایی روی گره i نسبت به جابجایی uq خواهد بود. این دو پارامتر به ترتیب 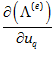 و
و 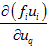 می باشند.
می باشند.
مشتق انرژی کرنشی المان نسبت به جابجایی گره ها
برای یافتن 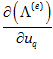 از یادآوری رابطه انرژی کرنشی در المان e زیر شروع می کنیم:
از یادآوری رابطه انرژی کرنشی در المان e زیر شروع می کنیم:
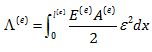
با فرض ثابت بودن E و A در هر المان رابطه به شکل زیر در می آید:
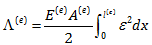
حال ازاین رابطه نسبت به uq مشتق می گیریم:
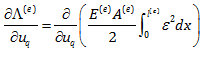
با توجه به ثابت بودن E و A می توان نوشت:
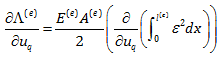
از طرفی چون پارامتر u نسبت به x وابسته نیست می توان مشتق را داخل انتگرال برد. پس داریم:
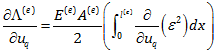
و در ادامه با مشتق گیری از ترم داخل انتگرال خواهیم داشت:
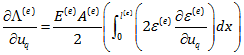
همان طور که می بینید مشتق انرژی کرنشی المان e نسبت به جابجایی گره ها به کرنش المان e و مشتق آن نسبت به جابجایی گره ها وابسته است. دقت کنید q=1,2,3,…,i,…,j,…n بوده و uq جابجایی گره q می باشد و ما بایستی در نهایت رابطه فوق را برای تمام q ها بدست آوریم.
از قبل روابط زیر را برای ε داشتیم:
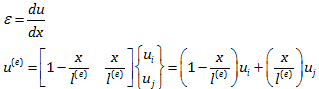
بنابراین برای کرنش المان e و مشتق آن نسبت به جابجایی گره q داریم:
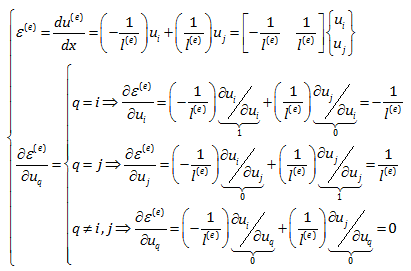
دقت کنید ما در اینجا با المانی با دو گره i و j مواجهیم. با توجه به اینکه مقدار q از 1 تا n تغییر خواهد کرد پاسخ ها بسته به اینکه q برابر i، j یا هر مقداری خلاف این دو باشد تغییر خواهد کرد که در بالا محاسبه شد. پس از استخراج این روابط که به شکل خلاصه در پایین نمایش داده شده است.
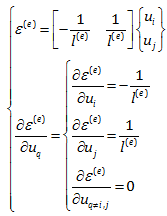
چیزی که مشهود است این است که کرنش و مشتق آن هیچ کدام وابستگی به x ندارند. بنابراین می توان این دو ترم را از انتگرال خارج نمود.
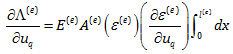
به این ترتیب مشتق انرژی کرنشی المان e در بالا به راحتی به شکل زیر درآمده و می توان در همین مرحله از شر انتگرال خلاص شد.
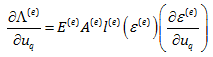
با جاگذاری ε(e) و مشتق آن، البته با در نظر گرفتن مقدار q در رابطه بالا به شکل جدیدی از معادلات که در زیر نشان داده شده است می رسیم.
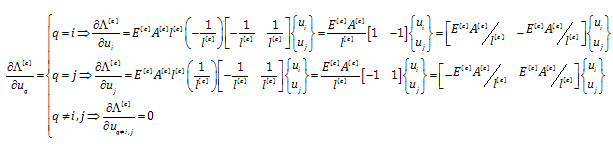
دقت کنید مفهوم عبارت آخر این است مشتق انرژی کرنشی نسبت به گره هایی که به المان وصل نیستند صفر است. پس در محاسبات کافی است تنها به گره های اطراف المان توجه کنیم.
به این ترتیب مشتق انرژی کرنشی المان e نسبت به جابجایی گره ها در فرم ماتریسی به شکل زیر خواهد بود:
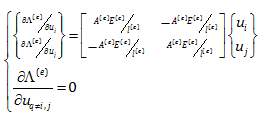
برای سادگی محاسبات یک تعریف جدید برای المان e با مشخصات A، E و l ارائه می دهیم و آن اینکه ترم A(e)E(e)/l(e) را با k(e) نام گذاری می کنیم. به این ترتیب معادلات بالا به شکل زیر در می آیند:
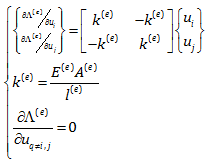
یاداور می شویم که ما به دنبال مشتق انرژی کرنشی کل نسبت به جابجایی گره ها بودیم. اکنون برای دیدن کل مسئله و محاسبه مشتق انرژی کرنشی کل (Λ(G)) بهتر است ابتدا به المان e بصورت کلی (Global) نگاه کنیم. بدین منظور در رابطه مشتق انرژی کرنشی المان e نسبت به جابجایی uq، مقادیر q را از 1 تا n جایگذاری می کنیم. همچنین همزمان همه جابجایی ها از u1 تا un را نیز در نظر می گیریم.
بنابراین معادلات را در قالب ماتریسی و به شکلی که در پایین می بینید تشکیل دهیم.
این مقاله برای کاربران سایت بصورت رایگان درنظر گرفته شده است. برای دسترسی کامل به آن و سایر مطالب این وب سایت لازم است از طریق گزینه زیر ثبت نام نمایید.
در صورتی که قبلا عضو سایت شده اید با کلیک روی دکمه زیر وارد شوید.
