در مقاله های قبل روی یک مسئله تک بعدی کار کردیم و معادلات المان محدود را برای آن استخراج کردیم. در این مقاله به منظور حل مسائل دوبعدی این معادلات را تعمیم می دهیم. اما پیش از این، جنبه های گسترش مسائل المان محدود را مورد بررسی قرار می دهیم.
جنبه های گسترش یک مسئله
نوع مسئله و نوع معادلات حاکم
می دانیم بر این اساس که نوع مسائل، استاتیک، دینامیک، ارتعاشات، انتقال حرارت و یا ترمودینامیکی باشند، روابط و معادلات حاکم بر سیستم متفاوت خواهد بود که تا کنون ما روی مسائل استاتیکی کار کردیم. علاوه بر نوع مسئله، خطی یا غیرخطی بودن معادلات در کنار ابعاد ماکروسکوپی یا میکروسکوپی آن ها نیز می تواند روی معادلات اجزاء محدود تاثیر داشته باشد.
فضای تعریف هندسه مسئله
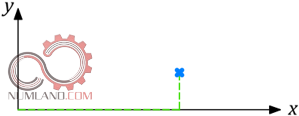
فضایی که هندسه مسئله در آن تعریف می شود می تواند یک بعدی (1D)، دوبعدی (2D)، سه بعدی (3D) و یا چندی بعدی باشد که این خود باعث تغییر در روابط خواهد شد. از این رو اگر بخواهیم مسائل را در حوزه استاتیکی، دینامیکی و غیره بررسی کنیم لازم است، ببینیم ابعاد هندسه مسئله از چه جهاتی قابل گسترش است یا به عبارت دیگر به چند بعد برای تعریف آن نیاز داریم. اولین هندسه ای که به ذهن می رسد یک جرم متمرکز است که بصورت یک نقطه (Point) قابل تعریف است. نقطه در فضاهای ابعادی مختلف می تواند تعریف شود. به عنوان مثال اگر مانند شکل 1 نقطه را روی یک محور مختصات در نظر بگیریم با توجه به اینکه محور مختصات یک بعد دارد، نقطه را در فضای یک بعدی تعریف کرده ایم.

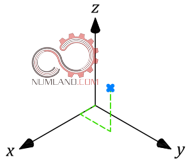
همچنین همانطور که در شکل های 2 و 3 نشان داده شده است، امکان تعریف این نقطه در فضای دوبعدی و سه بعدی نیز وجود دارد.
از طرف دیگر برخی قطعات ماننده میله ها، تیرها، خرپاها و غیره، در روش اجزاء محدود می توانند بصورت یک منحنی یا سیم (Wire) تعریف شوند. اگر این منحنی یک خط باشد (مانند میله ای که در بخش های قبل بررسی کردیم) می تواند مانند شکل 4 روی یک محور مختصات یا فضای یک بعدی تعریف شود.

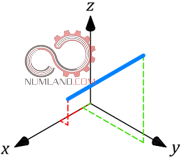
همچنین این منحنی ها می توانند در فضاهای دوبعدی و یا سه بعدی نیز مانند شکل های 5 و 6 بررسی شوند.

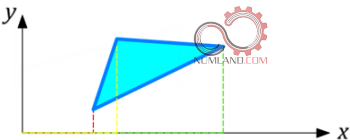
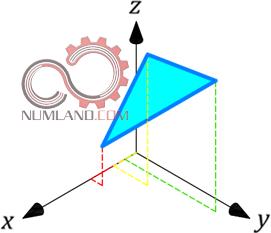
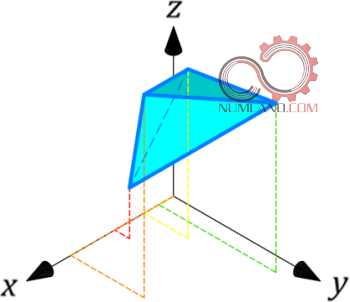
سومین هندسه ای که در مسائل اجزاء محدود قابل تعریف است پوسته (Shell) می باشد. با این هندسه می توان قطعات نازک نظیر ورق، مخزن و قطعاتی ازین دست را شبیه سازی نمود. طبیعتاً پوسته در یک بعد قابل تعریف نیست و مانند شکل های 7 و 8 لازم است در دو یا سه بعد بررسی شود.
آخرین هندسه ای که احتمالا در مسائل با آن مواجه هستیم جسم توپر (Solid) است. اکثر قطعاتی که در مسائل شبیه سازی می کنیم از این نوع هستند و همانطور که در شکل 9 مشخص شده است تنها می توان آن ها در فضای سه بعدی مدل کرد.
مفهوم درجه آزادی و فضای تعریف آن ها
در مقالات قبل و بررسی میله در حال کشش، روی هر گره از مدل اجزاء محدود، یک جابجایی در نظر گرفته شد. به عبارت دیگر عنوان شد که گره ni می تواند جابجایی ui را داشته باشد. به پارامتر جابجایی که به گره اجازه می دهد در یک جهت خاص حرکت کند درجه آزادی گره گفته می شود. در مسئله میله در حال کشش، فرض شد گره ها آزادند و تنها در یک جهت جابجا شوند که با توجه به اینکه در واقعیت نیز میله تنها در راستای خود کشیده یا فشرده (جابجا) می شود، این فرض درست بود.
اما مسائل از حیث درجات آزادی نیز قابل گسترش هستند. درجه آزادی در دسته ای از مسائل اسکالر است با این مفهوم که مقدار برای آن مهم است و جهت اهمیت ندارد. به عنوان مثال دما در مسائل انتقال حرارت از این نوع درجات آزادی است. درجه آزادی های برداری که بیشتر در مسائل مکانیکی با آن مواجه هستیم شامل سرعت، شتاب، جابجایی و… می باشند. در برخی مسائل نیز بسته به شرایط ممکن است معادلات مستقیماً بر اساس تنش و کرنش نوشته شود که در آن صورت درجه آزادی به صورت تانسوری خواهد بود.
معمولا درجات آزادی مسائلی که در علم مهندسی بررسی می شود از جنس بردار هستند لذا می توان گستردگی یک مسئله را از این حیث نیز بررسی نمود. مثلا درجه آزادی در درس قبل بصورت جابجایی تعریف شده بود لذا از جنس بردار بود. پس با توجه به اینکه گره ها فقط در راستای میله جابجا می شدند، همانند شکل 10 جابجایی گره ها را تنها در راستای یک محور (محور x) بررسی کردیم.
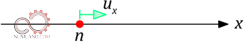
اما همانطور که در شکل های 11 و 12 نشان داده شده است جابجایی گره در دو یا سه بعد نیز قابل تعریف است.
این مقاله برای کاربران سایت بصورت رایگان درنظر گرفته شده است. برای دسترسی کامل به آن و سایر مطالب این وب سایت لازم است از طریق گزینه زیر ثبت نام نمایید.
در صورتی که قبلا عضو سایت شده اید با کلیک روی دکمه زیر وارد شوید.
