در مقاله قبل در رابطه با مسائل مهندسی صحبت کردیم و گفتیم دانش پایه ای دروس دانشگاهی تنها بخش کوچکی از مسائل دنیای واقعی را می تواند حل کند. همچنین راهکاری که در آنجا برای حل مسائل پیچیده مهندسی ارائه شد شامل تبدیل آن ها به قطعات کوچکتر و یافتن ارتباط بین آنها بود. همانطور که دیدید برای حل اینگونه مسائل نیاز داریم تا آنها را گسسته کنیم. یکی از روش هایی که با استفاده از همین نگرش به حل مسائل کمک می کند روش های اجزای محدود است. در این روش، ما عملا مسائل پیچیده را به تعداد زیادی قطعات کوچکتر که به آنها المان گفته می شود تقسیم می کنیم. لازم به ذکر است از این جهت به این روش، المان محدود می گویند که تعداد المان ها روی یک مسئله خاص مشخص است.
در صورت مشخص شدن رفتار گره های روی المان، قادر به تحلیل رفتار درون آن خواهیم بود. برای این کار نیاز داریم ابتدا معادلات حاکم بر المان ها را بررسی کنیم. به عنوان مثال اگر المانی به صورت یک خط داریم لازم است ابتدا ارتباط بین دونقطه ابتدا و انتها و نحوه وصل شدن آنها را به هم بیابیم تا بتوانیم روابط درون المانها را پیدا کنیم. به طور کلی حل یک مسئله پیچیده شامل یافتن روابط بین المانها، مونتاژ و نهایتا حل آنها خواهد بود.
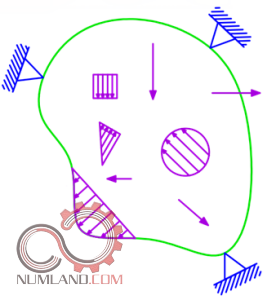
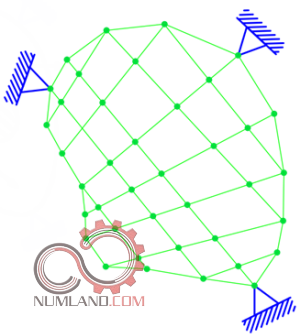
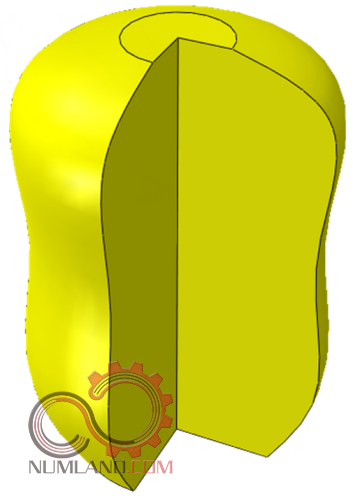
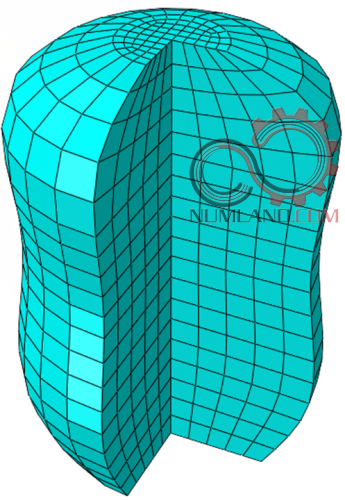
علاوه بر این مانند آنچه در شکل های 1 تا 6 دیده می شود با نحوه گسسته سازی یک میله یا یک سطح دو بعدی یا سه بعدی با بارگذاری، هندسه و متریال متغیر در بخش های مختلف آن آشنا شدید.


به این ترتیب همان طور که دیدید با تکنیک گسسته سازی می توانیم بسیاری از مسائل را تحلیل کنیم که درالمان محدود به آن شبکه بندی، المان بندی و یا مش بندی نیز گفته می شود. در این مرحله قصد داریم روابط حاکم بر المان ها و معادلات بین آنها را بدست آوریم. پس از مطالعه این مقاله شما قادر خواهید بود روند روش اجزاء محدود را درک نمایید.
رویکردهای روش اجزاء محدود برای یافتن معادلات المان ها
به منظور یافتن روابط المان ها دو رویکرد کلی داریم:
ا- رویکرد مستقیم (Direct Approach):
این تکنیک تنها برای مسائل ساده قابل استفاده است و از معادلات تعادل در آن استفاده می شود. در این روش مشابه آنچه در دروس مقاومت مصالح و استاتیک دیدید روابط المان ها را با مقطع زدن به دست می آوریم. با توجه به این موضوع این روش خیلی کاربردی نیست چرا که با در نظر گرفتن مقاله قبل، با پیچیده شدن مسائل، دیگر قادر نخواهیم بود به راحتی ازین روش های ابتدایی برای تحلیل مسائل استفاده کنیم. اما برای فهم روش اجزای محدود در ادامه یک مثال را با این روش حل خواهیم کرد.
2- رویکرد روش های عددی (Approach of Numerical Methods):
این روش بصورت کلی برای حل تمامی مسائل مهندسی مکانیک کاربرد دارد. در این روش ابتدا با در نظر گرفتن شرایط مرزی، معادلات حاکم بر سیستم که معمولا بصورت معادلات دیفرانسیل هستند استخراج می شود. از آنجا که معمولا حل این معادلات سخت است به این حالت از معادلات Strong Form گفته می شود. در ادامه اما این معادلات به یک حالت ساده تر و قابل حل تر که به آن Weak Form می گویند تبدیل می شوند. در نهایت نیز با استفاده از روش های عددی (Numerical Methods) برای این حالت یک جواب مناسب تخمین زده می شود. همانگونه که ذکر شد، دسته بزرگی از مسائل پیچیده را با این رویکرد می توان حل کرد.
رویکرد مستقیم برای استخراج معادلات المان ها در مسائل الاستیک خطی
به عنوان اولین مثال، کشش الاستیک خطی یک میله در یک بعد را به عنوان ساده ترین نوع مسائل مهندسی مکانیک در نظر بگیرید. به دلیل نازک بودن، مقاومت میله ها در برابر خمش، برش، پیچش قابل چشم پوشی است. لذا در آن ها فقط نیروی داخلی محوری بررسی می شود، از اینرو میله ها را در محاسبات مشابه فنر کششی-فشاری می دانند. همانطور که در شکل 7 نشان داده شده است این میله از سه بخش تشکیل شده که هر بخش سطح مقطع و متریال مخصوص به خود را دارد.
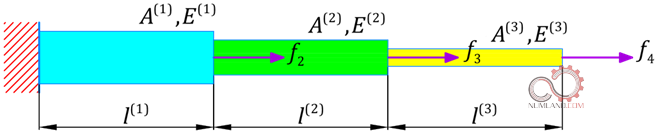
در واقع مسئله را میتوان سه میله جدا از هم فرض کرد که به هم متصل شده اند و در نقاط اتصال آنها نیروهای کششی وارد می شود. سطح مقطع در هر بخش با A، مدول الاستیسیته با E و طول آن با l نمایش داده می شود. برای حل این مسئله همانطور که در شکل 8 می بینید میله را از نقاط جدایش گسسته می کنیم. البته نقاط بیشتری هم در طول هر بخش می توان در نظر گرفت اما با توجه به خطی بودن رابطه جابجایی، یک المان برای هر بخش کافیست. به مرور با دنبال کردن این مقاله و مشاهده معادلات حاکم بر المان ها می توانید به مفهوم خطی بودن و دلیل انتخاب این تعداد از المان ها پی ببرید.

همانطور که در شکل 9 نشان داده شده نیروهایی که روی هندسه این مسئله اعمال می شود باعث ایجاد جابجایی هایی در نقاط جدایش می شوند که با u نمایش داده شده است.

اکنون برای تحلیل دقیق تر، یکی از المان ها با طول l، متصل به گره های ni و nj، مانند آنچه در شکل 10 نشان داده شده است را در نظر می گیریم و با حرف e نمایش می دهیم.
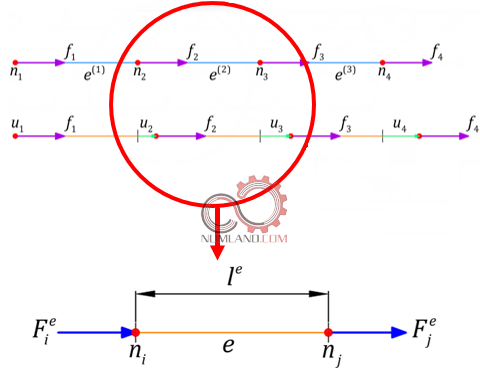
همان طور که از درس استاتیک می دانیم وقتی یک بخش از مسئله را از هندسه جدا می کنیم نیروهای معادل آن را باید به آن بخش اعمال کنیم. این نیروها در شکل با Fie و Fje نشان داده شده است. دقت کنید جهت نیروها در جهت مثبت محور مختصات فرض شده است. معادله تعادل برای این المان به شکل زیر نوشته می شود:
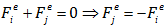
همان طور که در شکل 11 نشان داده شده نیروی داخلی المان که با Pe نمایش داده می شود نیز با مقطع زدن در طول المان به دست می آید.

به این ترتیب از معادله تعادل جدید داریم:
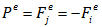
از طرفی طبق تعریف، تنش در المان برابر نیروی داخلی در واحد سطح می باشد.
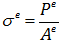
همان طور که قبلا گفته شد اعمال نیرو باعث ایجاد جابجایی در نودهای المان خواهد شد. بنابراین با اعمال نیرو، المان به طول جدیدی خواهد رسید که در شکل 12 با 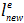 نشان داده شده است.
نشان داده شده است.
این مقاله برای کاربران سایت بصورت رایگان درنظر گرفته شده است. برای دسترسی کامل به آن و سایر مطالب این وب سایت لازم است از طریق گزینه زیر ثبت نام نمایید.
در صورتی که قبلا عضو سایت شده اید با کلیک روی دکمه زیر وارد شوید.
