شکاف بین توانایی مهندسین بعد از گذراندن دروس پایه و سطح مسائل واقعی
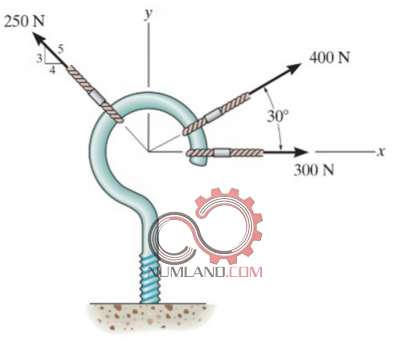
به طور کلی به منظور فهم تدریجی مباحث مهندسی، دانشجویان، و به طور خاص دانشجویان مهندسی مکانیک و عمران، ابتدا با مسائل ساده روبرو می شوند. در ادامه نیز با توجه به دروس مختلف مهندسی و مباحثی که در آن ها مطرح می شود سطح این مسائل رفته رفته پیچیده تر خواهد شد. به عنوان مثال درس استاتیک اغلب با تحلیل تیرهایی تحت بارگذاری های مختلف شروع می شود. که نمونه هایی ازین دست مسائل را در شکل های 1 تا 4 میبینید.

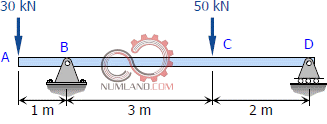
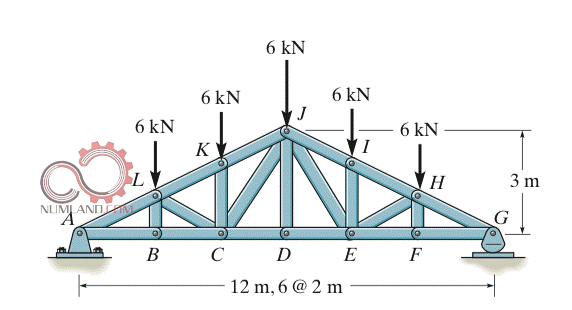
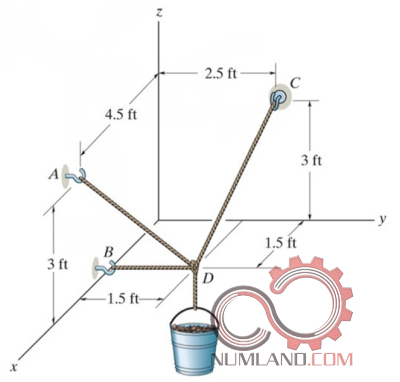
در مراحل بعدی در درس استاتیک، همان طور که در شکل های 5 و 6 می بینید با مسائلی نظیر خرپاها مواجه می شویم که برای تحلیل آنها از تکنیک هایی مانند مقطع زدن و تحلیل استاتیکی در مفاصل خرپا استفاده می کنیم.
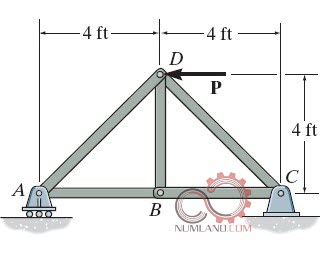
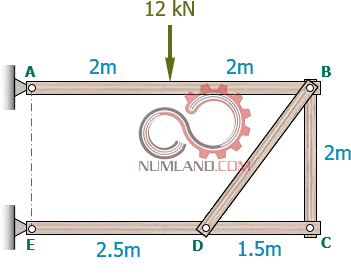
همان طور که در شکل های 7 و 8 دیده می شود خرپاها می توانند به شکل های پیچیده تری با بارگذاری های متنوع تر نیز دیده شوند.
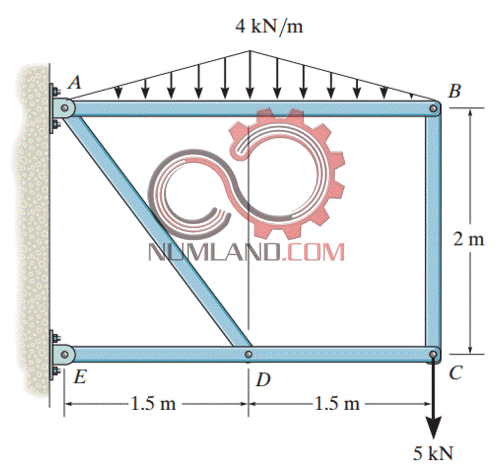
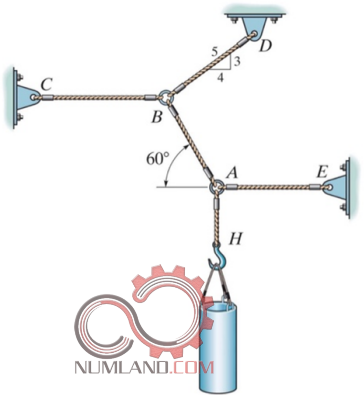
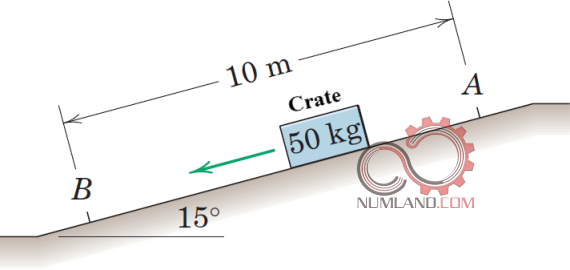
از طرف دیگر ممکن است با مسائلی به ظاهر پیچیده تر نیز سرورکار داشته باشیم تا فهم ما از استاتیک گسترش یابد. مثلا تحلیل کابل ها به عنوان اجزائی که فقط می توانند کشیده شوند و فشار را تحمل نمی کنند کم کم مفهوم تاثیر ماده در مسائل مهندسی را به ما آموزش می دهند. شکل های 9 تا 11 نمونه هایی از این موارد را نشان می دهد.
در دروس پیشرفته تری چون مقاومت مصالح مباحث تنش، کرنش و خیز تیر نیز به این مباحث اضافه می شود که سطح دید ما را نسبت به مسائل مهندسی مکانیک گسترش خواهد داد.
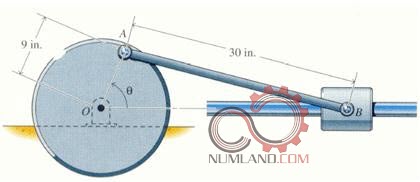
علاوه بر همه اینها، وقتی بخواهیم اجسام در حال حرکت را تحلیل کنیم، با مسائل ریز و درشت دینامیکی، که نمونه هایی از آن ها در شکل های 12 تا 14 نشان داده شده اند، روبرو می شویم که با حل آن ها به درک این مسائل خواهیم رسید.
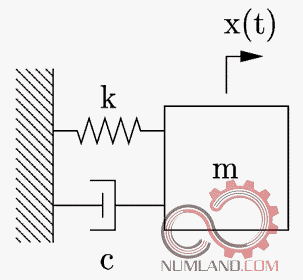
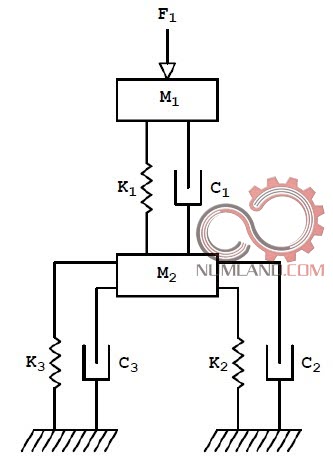
در مسائل ارتعاشاتی نیز هدف یافتن رفتارهای جرم، فنر دمپر و اثر آن ها و ارتعاشات مربوطه روی سیستم است. در این بخش کم کم با مفهوم رزونانس و فرکانس های طبیعی سیستم آشنا خواهیم شد. علاوه بر این استخراج شکل مود هایی که در آنها رزونانس اتفاق می افتد را یاد می گیریم. نمونه هایی ازین مدل مسائل در شکل های 15 و 16 آورده شده است.
توجه داشته باشید اگر چه ممکن است در مقاطع بالاتر آموزش عالی مسائل پیشرفته تری ازین دست را تحلیل، کنیم اما باز هم تا مسائل واقعی دنیای صنعت، جایی که قرار است ما با حل مسائل بهره وری ایجاد کنیم، فاصله داریم. ازین رو اگر در آینده بخواهید به عنوان یک مهندس، مسائل واقعی و صنعتی دنیای مهندسی را تحلیل کنید، متاسفانه دانش کسب کرده از دروس دانشگاهی به تنهایی کارایی زیادی ندارند.
به عنوان مثال مواردی را در نظر بگیرید که به عنوان یک مهندس معمار در طراحی و استحکام سازه های پیچیده معماری با آن مواجه هستید. قطعا اگر بخواهید این مسئله را با علمی که از استاتیک و مقاومت به دست آورده اید تحلیل کنید به بن بست خواهید رسید. چرا که اول از همه به راحتی نمی توان المان های تشکیل دهنده یک سازه را به تیرها و میله هایی که تحلیل آن ها را در دروس مذکور یاد گرفته ایم تبدیل کنیم. همچنین محاسبه این حجم از المان بصورت تک به تک با توجه به انرژی و زمانی که بایستی صرف آن کرد، در صنعت قابل توجیه نیست.

یا مواردی که در صنایع خودرو و در مواجه با قطعات متحرک پیچیده با آن برخورد می کنید. در این موارد به سادگی و تنها با تکیه بر علوم ساده مهندسی نمی توان مواردی چون استحکام، تغییر شکل، خزش و تنش سازه ها را تحلیل کرد.
این مقاله برای کاربران سایت بصورت رایگان درنظر گرفته شده است. برای دسترسی کامل به آن و سایر مطالب این وب سایت لازم است از طریق گزینه زیر ثبت نام نمایید.
در صورتی که قبلا عضو سایت شده اید با کلیک روی دکمه زیر وارد شوید.
