پس از فهم روند یافتن معادلات اجزاء محدود و تشکیل روابط مربوطه، اکنون آماده ایم تا از این روش برای حل مسئله میله در حال کشش (شکل 1) که روی آن کار کردیم استفاده نماییم.
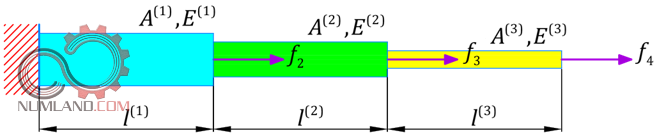
در ابتدا طبق روال گذشته میله را مانند شکل 2 گسسته کرده و نیروها و جابجایی ها را روی آن لحاظ می کنیم.
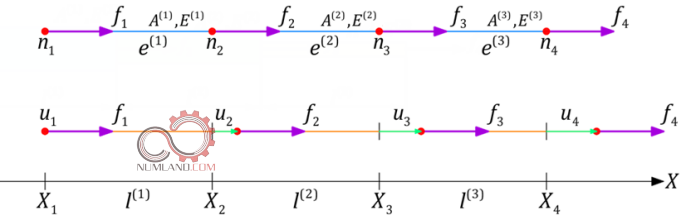
در مقاله قبل با در نظر گرفتن تئوری انرژی پتانسل کمینه، نشان دادیم بین نیرو های اعمالی، هندسه، مواد و جابجایی ها رابطه زیر بر قرار است:
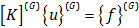
در این رابطه با توجه به شکل 2 و جابجایی ها و نیرو هایی که روی آن مشخص کرده ایم، می توانیم بردارهای 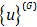 و
و 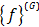 را به صورت زیر بنویسیم:
را به صورت زیر بنویسیم:
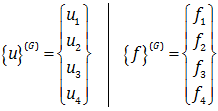
از طرفی گفتیم ماتریس سختی کل، از مونتاژ ماتریس سختی المان ها بدست می آید. بنابراین داریم:
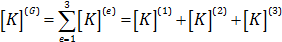
در این رابطه ماتریس های 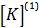 ،
، 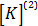 و
و 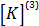 به ترتیب ماتریس های سختی المان های 1، 2 و 3 می باشد. با توجه به اینکه تعداد 4 جابجایی روی مدل اجزاء محدودی که در شکل 2 در نظر گرفته ایم و اینکه از قبل می دانیم تعداد سطر و ستون های ماتریس سختی برابر با این تعداد خواهد بود، برای استخراج ماتریس های سختی المان ها، ابعاد آن ها را 4×4 در نظر می گیریم.
به ترتیب ماتریس های سختی المان های 1، 2 و 3 می باشد. با توجه به اینکه تعداد 4 جابجایی روی مدل اجزاء محدودی که در شکل 2 در نظر گرفته ایم و اینکه از قبل می دانیم تعداد سطر و ستون های ماتریس سختی برابر با این تعداد خواهد بود، برای استخراج ماتریس های سختی المان ها، ابعاد آن ها را 4×4 در نظر می گیریم.
اکنون برای استخراج ماتریس سختی المان اول با توجه به توضیحات بالا داریم:
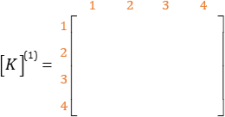
همان طور که می دانید گره های 1 و 2 به این المان وصل هستند بنابراین تنها مولفه های مشترک سطر و ستون 1 و 2 مقدار خواهند داشت و باقی مولفه ها نیز صفر خواهند بود. پس:
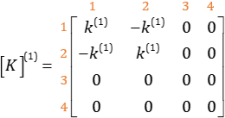
همچنین طبق تعریف داشتیم:
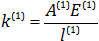
به همین ترتیب ماتریس سختی المان های دوم و سوم را نیز تشکیل می دهیم.
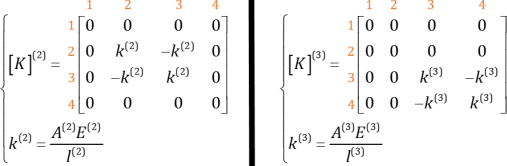
به این ترتیب 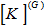 به شکل زیر خواهد بود:
به شکل زیر خواهد بود:
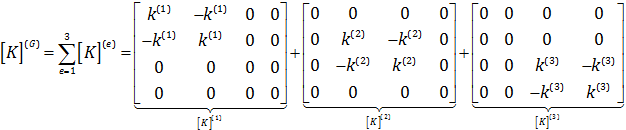
در نتیجه:
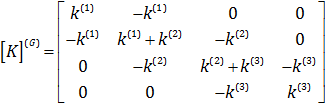
اکنون تمام ترم های معادله اجزاء محدود تشکیل شده است. پس داریم:
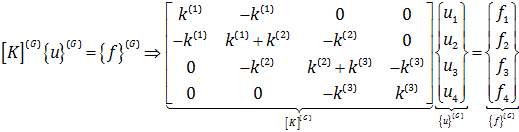
در این رابطه مقادیر u2، u3، u4 و f1 مجهول هستند که با یافتن آن ها عملا مسئله حل خواهد شد. لازم به توضیح است که در مرحله اول مستقیما جابجایی u ها که مجهولات ما هستند را پیدا می کنیم، و در مراحل بعدی نتایج غیر مستقیم نظیر کرنش، تنش و نیروی عکس العمل را محاسبه می نماییم.
در ادامه به بررسی یک مثال با شرایط شکل 3 می پردازیم:

در نظر داشته باشید به منظور سادگی محاسبات، در کل میله تنها یک سطح مقطع و یک مدول الاستیسیته لحاظ شده است. همچنین سه نیروی برابر f روی این گره ها اعمال می شوند و طول هر سه بخش برابر l است. گسسته سازی روی این میله مطابق با شکل 4 خواهد بود:

دقت کنید R نیروی عکس العمل تکیه گاه سمت چپ است. همچنین جابجایی گره ای که روی تکیه گاه قرار دارد برابر صفر خواهد بود (u1=0).
معادلات زیر را برای این مسئله تشکیل می دهیم:
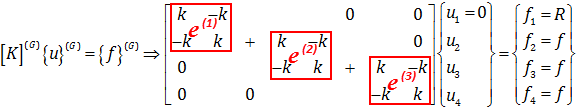
که در آن 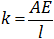 است. دقت کنید همانطور که قبلا گفته شد ماتریس سختی کل از مونتاژ ماتریس سختی های المان ها تشکیل می شود. به این ترتیب معادله روش اجزاء محدود به شکل ماتریسی زیر نوشته می شود. در همین مرحله شرایط مرزی (u1=0) را اعمال می کنیم.
است. دقت کنید همانطور که قبلا گفته شد ماتریس سختی کل از مونتاژ ماتریس سختی های المان ها تشکیل می شود. به این ترتیب معادله روش اجزاء محدود به شکل ماتریسی زیر نوشته می شود. در همین مرحله شرایط مرزی (u1=0) را اعمال می کنیم.
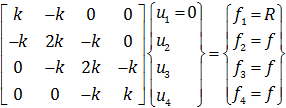
محاسبه جابجایی گره ها (نتایج مستقیم)
با ضرب u1=0 در ستون اول ماتریس [K]، این ستون از محاسبات خارج می شود. از طرفی معادله حاصل از ضرب سطر اول ماتریس [K] در ماتریس 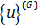 نیز معادله ارزشمندی در راستای مجهولات جابجایی نمی دهد، چرا که مقدار R در آن مجهول خواهد ماند. لذا این سطر نیز فعلا از محاسبات خارج می گردد. ترم های حذف شده بر اساس صحبت هایی که شد بدین صورت خواهد ماند.
نیز معادله ارزشمندی در راستای مجهولات جابجایی نمی دهد، چرا که مقدار R در آن مجهول خواهد ماند. لذا این سطر نیز فعلا از محاسبات خارج می گردد. ترم های حذف شده بر اساس صحبت هایی که شد بدین صورت خواهد ماند.
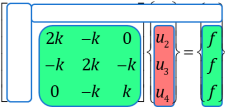
در روابط بالا، آیتم های معلوم به رنگ سبز و آیتم های مجهول با رنگ قرمز مشخص شده اند. با نوشتن این آیتم ها به شکل زیر می توانیم مجهولات را بدست آوریم:
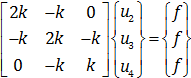
با معکوس کردن ماتریس مربعی باقیمانده از 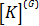 به راحتی به معادله زیر می رسیم.
به راحتی به معادله زیر می رسیم.
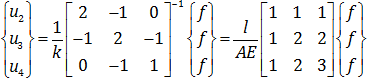
با ضرب دو ماتریس آخر مجهول u به شکل زیر دست می آید.
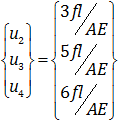
حال اگر u1 را که از قبل مقدار آن را می دانستیم به این جمع اضافه کنیم، مقدار جابجایی کل گره ها را با هم خواهیم داشت:
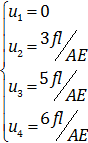
در نظر داشته باشید با توجه به اینکه معادلات حاکم بر المان ها دقیقا روی معادلات حاکم بر هر بخش از میله می افتد، در این نوع از مسائل حل تخمینی، نتایج کاملا دقیق را به ما ارائه داد.
بدست آوردن نتایج غیر مستقیم در روش اجزاء محدود
محاسبه جابجایی های درون المان ها
پس از بدست آوردن جابجایی روی گره ها، جابجایی درون المان ها نیز به راحتی قابل محاسبه است. به یاد داریم که جابجایی درون المان e که به گره های ui و uj متصل است، از رابطه زیر بدست می آید:
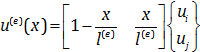
پس با در نظر گرفتن جابجایی گره های مربوط به هر المان داریم:
این مقاله برای کاربران سایت بصورت رایگان درنظر گرفته شده است. برای دسترسی کامل به آن و سایر مطالب این وب سایت لازم است از طریق گزینه زیر ثبت نام نمایید.
در صورتی که قبلا عضو سایت شده اید با کلیک روی دکمه زیر وارد شوید.
