در این درس علاوه بر مرور و تسلط بر تکنیک های درس قبل وآموزش روش متفاوت حل مساله، به رفع هشدارهای نرم افزار در حل مساله قبل می پردازیم.
انتظار ما از شما بعد از مطالعه این درس
1- رفع هشدارهای تحلیل درس دوم
شرح مختصر مسئله:
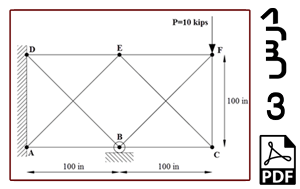
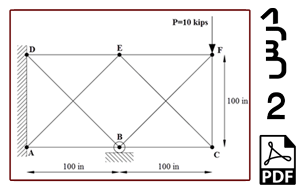
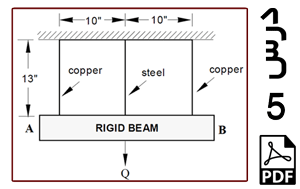
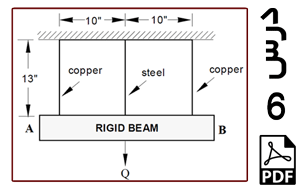
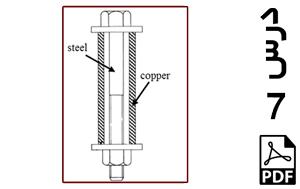
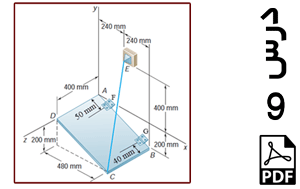
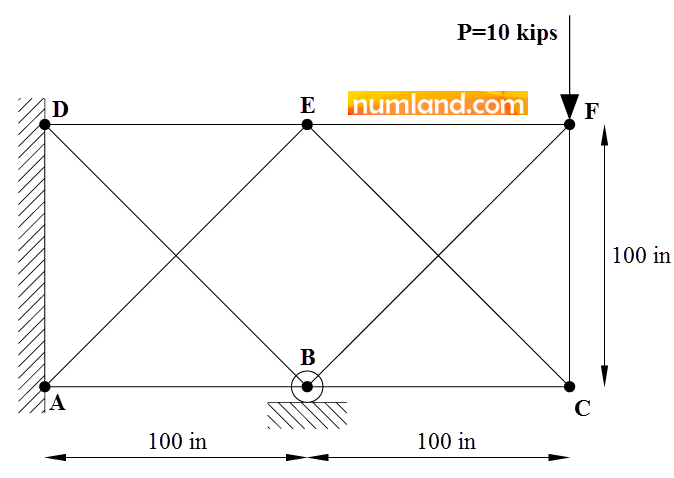
خرپای دوبعدی نشان داده شده در شکل 1 را در نظر بگیرید. این خرپا متشکل از 9 عضو است. دو عضو BF و CE و همچنین اعضای AE و BD بدون اینکه یکدیگر را قطع کنند از روی هم عبور کرده اند یعنی هر یک از این اعضا فقط شامل یک المان هستند. نقاط A و D در یک دیوار عمودی قرار دارند در نتیجه امکان جابه جایی در هیچ راستایی را ندارند. نقطه B تکیه گاه غلتکی است. عضو CF در اثر خطای ساخت به اندازه 0.1 in کوتاه تر از 100 in (یا همان طول 99.9 in) است در نتیجه ابتدا آن را بین نقاط F و C جاسازی می کنیم که در نتیجه این کار، پیش تنشی در سازه ایجاد می شود. نیروی عمودی P به نقطه F اعمال شده است. نقطه تکیه گاهی B به اندازه 0.05 in به سمت پایین کشیده می شود و در همان نقطه نگهداشته می شود. کل سازه به اندازه 50 oF گرم می شود در نتیجه تنشهای حرارتی در آن ایجاد می شود. هدف، به دست آوردن میزان تنش در عضو CF و نیروی تکیه گاهی RB و مقایسه آنها با نتایج مرجع [1] می باشد. طول اعضا بر حسب اینچ و جنس آنها از فولاد با مدول الاستیسیته 30×106 psi و ضریب انبساط حرارتی ![]() و سطح مقطع 3.33333 in2 است.
و سطح مقطع 3.33333 in2 است.
با خرید این درس و دسترسی به تمام مطالب آن می توانید به محیط تحلیل مسائل استاتیک در نرم افزار آباکوس مسلط شده و مسائل دانشگاهی و صنعتی خود را در این حوزه به راحتی بررسی نمایید.
فراموش نکنیم، دانشی که در درس استاتیک فراگرفته اید تنها شما را با مبحث استاتیک در مهندسی مکانیک آشنا کرده است. اما خبر خوب این است که با تعمیم دانشی که در این درس فرا گرفته اید به روش اجزاء محدود و نرم افزار آباکوس، که محبوبترین و مجهزترین ابزار در این حوزه است، می توانید به راحتی از پس مسائل صنعتی و پروژه های پیچیده دانشگاهی برآیید.
از شما دعوت می کنیم با مطالعه بخش اولیه این درس نکات مهمی از فرایند شبیه سازی مسائل استاتیکی در نرم افزار آباکوس را بیاموزید.
در صورتی که علاقه مند به ادامه فراگیری این آموزش و نکات تکمیلی آن هستید؛ پس از ثبت نام، روی دکمه افزودن به سبد خرید در همین صفحه کلیک نمایید.