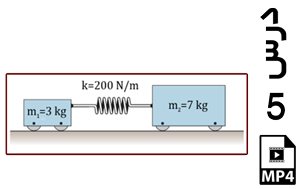
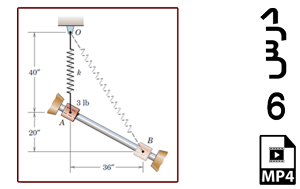
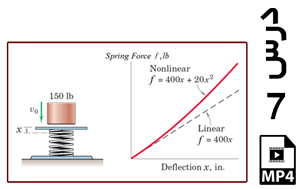
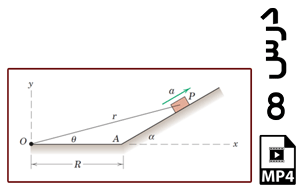
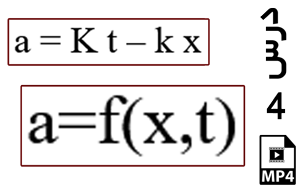در این مثال ذره ای در مبدا مختصات از حالت سکون در راستای x شروع به حرکت می کند. با داشتن رابطه شتاب ذره بر حسب زمان، هدف به دست آوردن جابجایی و سرعت ذره بر حسب زمان می باشد. با حل این مساله علاوه بر مرور تکنیک های مسائل قبل با مهارت های تعریف فنر خطی، تعریف Amplitude خطی و تعریف نیروی متمرکز در محیط آباکوس آشنا می شوید.
شرح مختصر مسئله:
ذره ای در مبدا مختصات از حالت سکون در راستای x شروع به حرکت می کند. شتاب ذره توسط رابطه زیر بیان می شود.
در این رابطه، K و k ثابتهای مثبت، x جابجایی ذره و t زمان است. هدف، به دست آوردن جابجایی و سرعت ذره بر حسب زمان و مقایسه آنها با نتایج مرجع [1] می باشد.
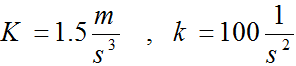
بعد از مطالعه این درس به مهارت های زیر مسلط خواهید شد:
1- تعریف فنر خطی
2- تعریف Amplitude خطی
3- تعریف نیروی متمرکز
با خرید این درس و دسترسی به تمام مطالب آن می توانید به محیط تحلیل مسائل دینامیک در نرم افزار آباکوس مسلط شده و مسائل دانشگاهی و صنعتی خود را در این حوزه به راحتی بررسی نمایید.
فراموش نکنیم، دانشی که در درس دینامیک فراگرفته اید تنها شما را با مبحث دینامیک در مهندسی مکانیک آشنا کرده است. اما خبر خوب این است که با تعمیم دانشی که در این درس فرا گرفته اید به روش اجزاء محدود و نرم افزار آباکوس، که محبوبترین و مجهزترین ابزار در این حوزه است، می توانید به راحتی از پس مسائل صنعتی و پروژه های پیچیده دانشگاهی برآیید.
از شما دعوت می کنیم با مشاهده بخش اولیه این درس نکات مهمی از فرایند شبیه سازی مسائل دینامیکی در نرم افزار آباکوس را بیاموزید.
در صورتی که علاقه مند به ادامه فراگیری این آموزش و نکات تکمیلی آن هستید؛ پس از ثبت نام، روی دکمه افزودن به سبد خرید در همین صفحه کلیک نمایید.